New AI:Single Epoch Learning (SEL)
We provide technology for training neural networks such as deep learning accurately in a short time.
Traditional training methods, such as Back Propagation (BP), adjust neural network parameters over and over again.
Our patented SEL provides sufficient training with just one adjustment.
In the conventional training method, the error is gradually reduced
by iterative calculation based on the gradient information of the error of the neural network.
On the other hand, this patented technology allows to reach nearly optimum solution
with a single algebraic calculation.
Therefore, the error can be reduced accurately without waste in calculation.
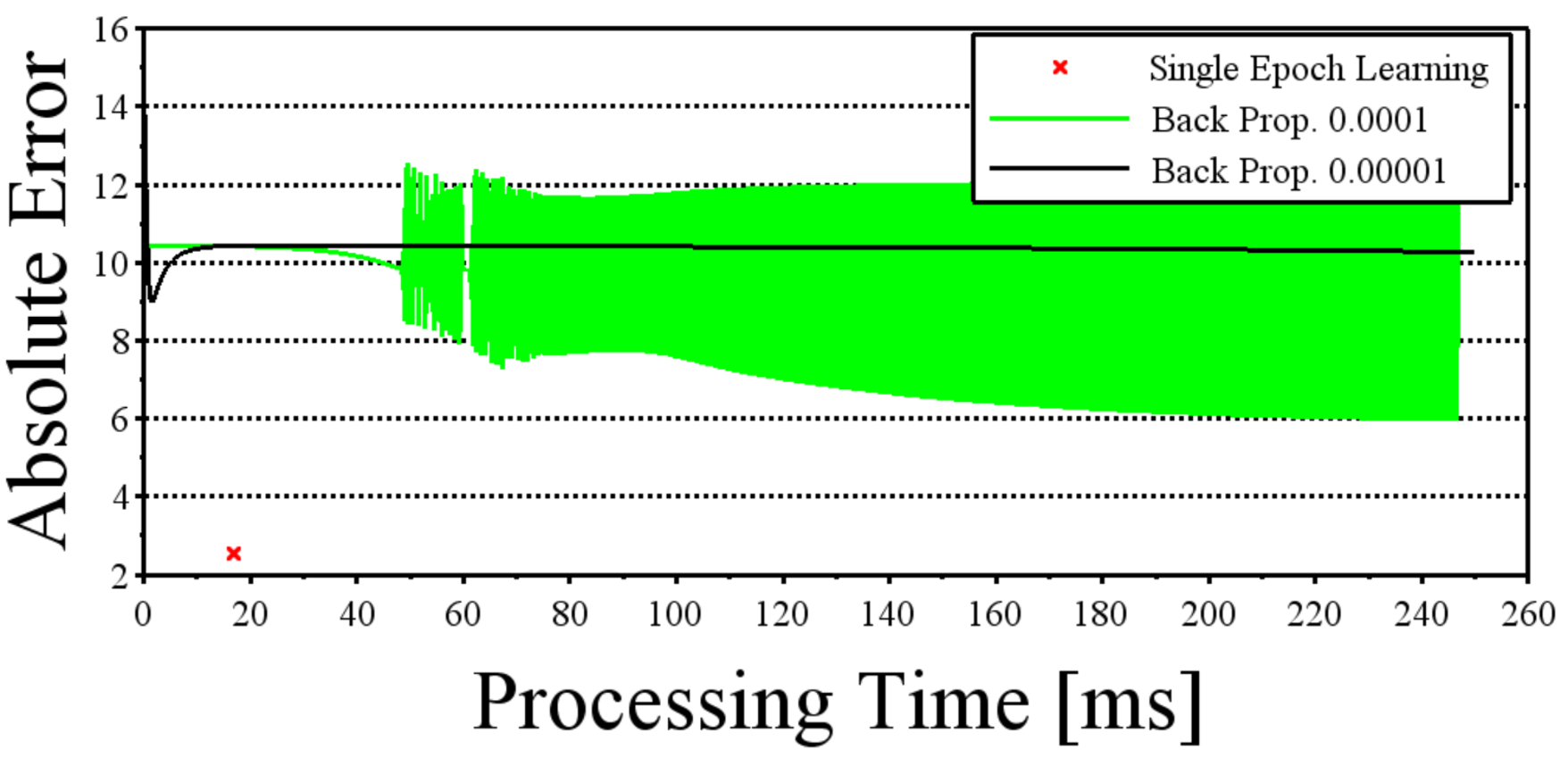
Fig.1 Error Comparison between SEL and BP (Yacht Hydrodynamics Data Set)
Performance Comparision
We evaluated the algorithms using the datasets in UCI Machine Learning Repository that frequently used for machine learning performance evaluation (Table 1).
| Data Set | Input Dimension |
Output Dimension |
Output Information |
Number of Training Data | Number of Test Data |
|---|---|---|---|---|---|
| 1. Airfoil Self-Noise Data Set | 5 | 1 | Scaled sound pressure level | 752 | 753 |
| 2. Computer Hardware Data Set | 8 | 1 | ERP | 104 | 105 |
| 3. Concrete Compressive Strength Data Set | 8 | 1 | Concrete compressive strength | 515 | 515 |
| 4. Online News Popularity Data Set | 58 | 1 | Shares | 19822 | 19822 |
| 5. Wine Quality Data Set (red) | 11 | 1 | Quality | 800 | 799 |
| 6. Wine Quality Data Set (white) | 11 | 1 | Quality | 2449 | 2449 |
| 7. Yacht Hydrodynamics Data Set | 6 | 1 | Residuary resistance | 154 | 154 |
Table 2 shows the absolute value error and calculation time when single epoch learning was performed with one thread on Intel Core i9-8950HK, where, xx-yy indicates that the number of nodes in Intermediate Layer 1 was xx and those in Intermediate Layer 2 was yy. For example, in Airfoil Self-Noize Data Set 20-20, Input Layer had 5 nodes, Intermediate Layer 1 had 20 nodes, Intermediate Layer 2 had 20 nodes, and Output Layer had 1 node. Every layer was fully connected. The activation functions were "Linear" for Output Layer and "Sigmoid" for the other layers. The values in parentheses in the tables are the learning time [ms], measured by C++ STL chrono.
| Data Set |
Int. Layer: None |
2 | 5 | 10 | 20 | 2-2 | 5-5 | 10-10 | 20-20 |
|---|---|---|---|---|---|---|---|---|---|
| 1. | 3.82 (3) |
3.83 (6) |
3.82 (10) |
3.68 (12) |
3.08 (22) |
3.75 (4) |
3.98 (12) |
3.72 (26) |
3.04 (72) |
| 2. | 23.4 (8) |
21.1 (15) |
17.7 (30) |
12.9 (14) |
80.2 (25) |
44.1 (23) |
24.1 (33) |
58.6 (19) |
56.5 (38) |
| 3. | 7.97 (11) |
8.18 (20) |
7.93 (20) |
7.50 (24) |
8.34 (35) |
12.3 (31) |
7.05 (26) |
7.54 (30) |
7.79 (64) |
| 4. | 5266 (231) |
3243 (614) |
3768 (1226) |
3992 (2243) |
5223 (4179) |
3217 (660) |
3225 (1323) |
3314 (2616) |
8.27E3 (5649) |
| 5. | 0.516 (9) |
0.525 (13) |
0.516 (23) |
0.521 (37) |
0.518 (59) |
0.717 (21) |
0.516 (29) |
0.527 (52) |
0.521 (102) |
| 6. | 0.579 (5) |
0.582 (24) |
0.579 (49) |
0.580 (68) |
0.579 (107) |
0.659 (33) |
0.579 (64) |
0.579 (107) |
0.635 (260) |
| 7. | 7.51 (2) |
7.50 (14) |
1.55 (42) |
5.91 (17) |
2.54 (17) |
7.31 (13) |
8.73 (20) |
2.18 (62) |
11.5 (27) |
The results of BP training are shown in Tables 3 and 4. These tables show the results at the time of 1000 learning epochs. From the comparison with Table 2, SEL reduced the error quicker with more accuracy. SEL also has adjustment-free feature of update rate (UR). BP is prone to fall in local optimums and sometimes gets error vibrations depending on its update rate. SEL does not take these problems.
| Data Set |
Int. Layer: None |
2 | 5 | 10 | 20 | 2-2 | 5-5 | 10-10 | 20-20 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | nan (82) |
5.70 (235) |
4.98 (395) |
5.77 (778) |
5.66 (1455) |
5.70 (442) |
5.70 (867) |
5.70 (2567) |
5.70 (4362) |
| 2 | nan (19) |
91.8 (46) |
93.0 (72) |
93.1 (122) |
93.1 (223) |
91.7 (68) |
93.0 (135) |
93.1 (281) |
93.3 (624) |
| 3 | nan (64) |
12.8 (185) |
12.8 (326) |
10.8 (580) |
12.8 (1086) |
12.8 (365) |
12.8 (531) |
12.8 (1301) |
12.8 (3817) |
| 4 | nan (1.3E4) |
3207 (3.5E4) |
3207 (5.8E4) |
2.73E11 (9.8E4) |
nan (1.6E5) |
3207 (3.8E4) |
3202 (6.9E4) |
2.90E30 (1.2E5) |
nan (2.3E5) |
| 5 | nan (128) |
0.747 (373) |
0.686 (668) |
0.562 (986) |
0.515 (1790) |
0.518 (420) |
1.34 (879) |
0.528 (1874) |
0.680 (4477) |
| 6 | nan (383) |
0.678 (1073) |
0.664 (2014) |
0.649 (3610) |
0.642 (6283) |
0.665 (1276) |
0.685 (2678) |
0.629 (5665) |
0.644 (1.3E4) |
| 7 | 11.4 (21) |
11.5 (48) |
11.5 (79) |
11.5 (136) |
11.3 (250) |
11.5 (66) |
11.4 (141) |
9.95 (300) |
13.7 (770) |
| Data Set |
Int. Layer: None |
2 | 5 | 10 | 20 | 2-2 | 5-5 | 10-10 | 20-20 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | nan (72) |
5.70 (229) |
4.91 (421) |
4.93 (795) |
5.70 (1478) |
5.70 (393) |
5.70 (857) |
5.70 (1848) |
5.70 (5910) |
| 2 | nan (19) |
93.1 (44) |
93.1 (72) |
93.1 (129) |
93.1 (241) |
93.1 (68) |
94.1 (133) |
94.6 (283) |
93.9 (688) |
| 3 | nan (67) |
12.6 (214) |
10.4 (326) |
12.4 (594) |
11.7 (1168) |
12.8 (447) |
12.8 (541) |
12.8 (1288) |
12.8 (3955) |
| 4 | nan (1.3E4) |
nan (3.5E4) |
nan (5.8E4) |
nan (9.5E4) |
nan (1.6E5) |
nan (3.6E4) |
nan (6.1E4) |
nan (1.1E5) |
nan (2.2E5) |
| 5 | nan (126) |
0.728 (399) |
0.739 (622) |
0.707 (1090) |
0.674 (1970) |
0.741 (432) |
1.34 (891) |
0.528 (1867) |
0.680 (4409) |
| 6 | nan (370) |
0.641 (1166) |
0.641 (1897) |
3.53E34 (3466) |
nan (5534) |
0.666 (1270) |
0.667 (2923) |
1.47E38 (7443) |
nan (1.2E4) |
| 7 | 10.4 (22) |
11.5 (47) |
11.5 (80) |
7.52 (135) |
7.50 (247) |
11.5 (67) |
11.5 (139) |
11.7 (300) |
11.5 (763) |